Uncertainty is fun. If we knew the result of sporting contests in advance, they’d be tedious. When we go to a footy game, we want there to be some decent chance that the underdogs might win.
It turns out, though, that footy has fewer games in which the result is very uncertain than other sports. To measure this, I’ve used bookmakers’ odds for various sports, shamelessly inspired by a post at FiveThirtyEight.1
In footy, there’s a flat distribution of expected outcomes, with plenty of games in which the home team is expected to win or lose comfortably. By contrast, a range of other sports have narrower distributions. They feature more games in which the probability is much closer to 50-50 – a tossup game. Footy has relatively few tossups, compared to other sports.
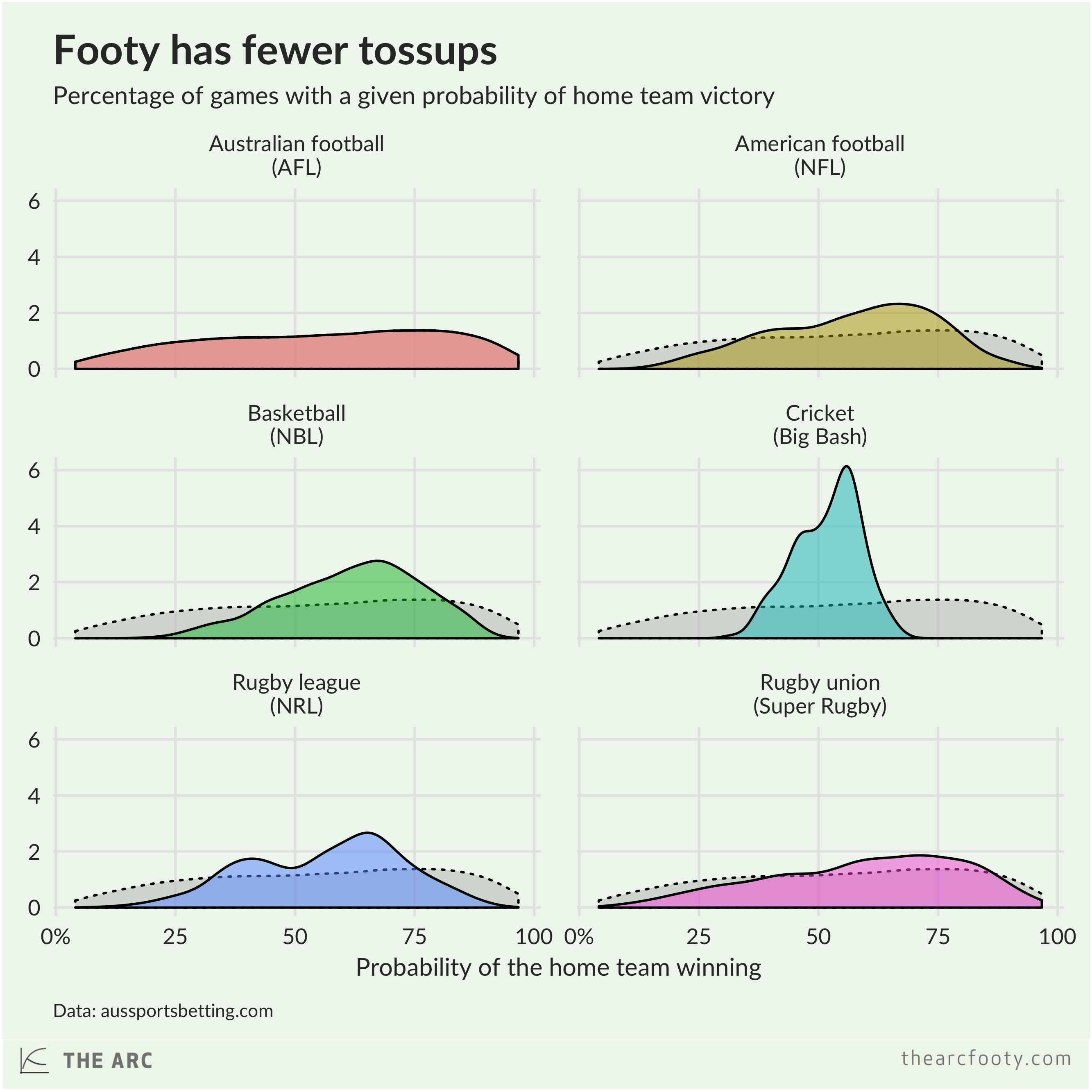
What do we mean by a tossup? Let’s take it to mean a game in which the home team is given somewhere between a 40% and 60% chance of winning by the bookies. Within that range, the outcome is close enough to 50-50 that we can call it a tossup. An overwhelming majority – 82.5% – of Big Bash cricket games are tossups, while only 23.7% of AFL footy games can be described that way. Other sports fall somewhere in between.
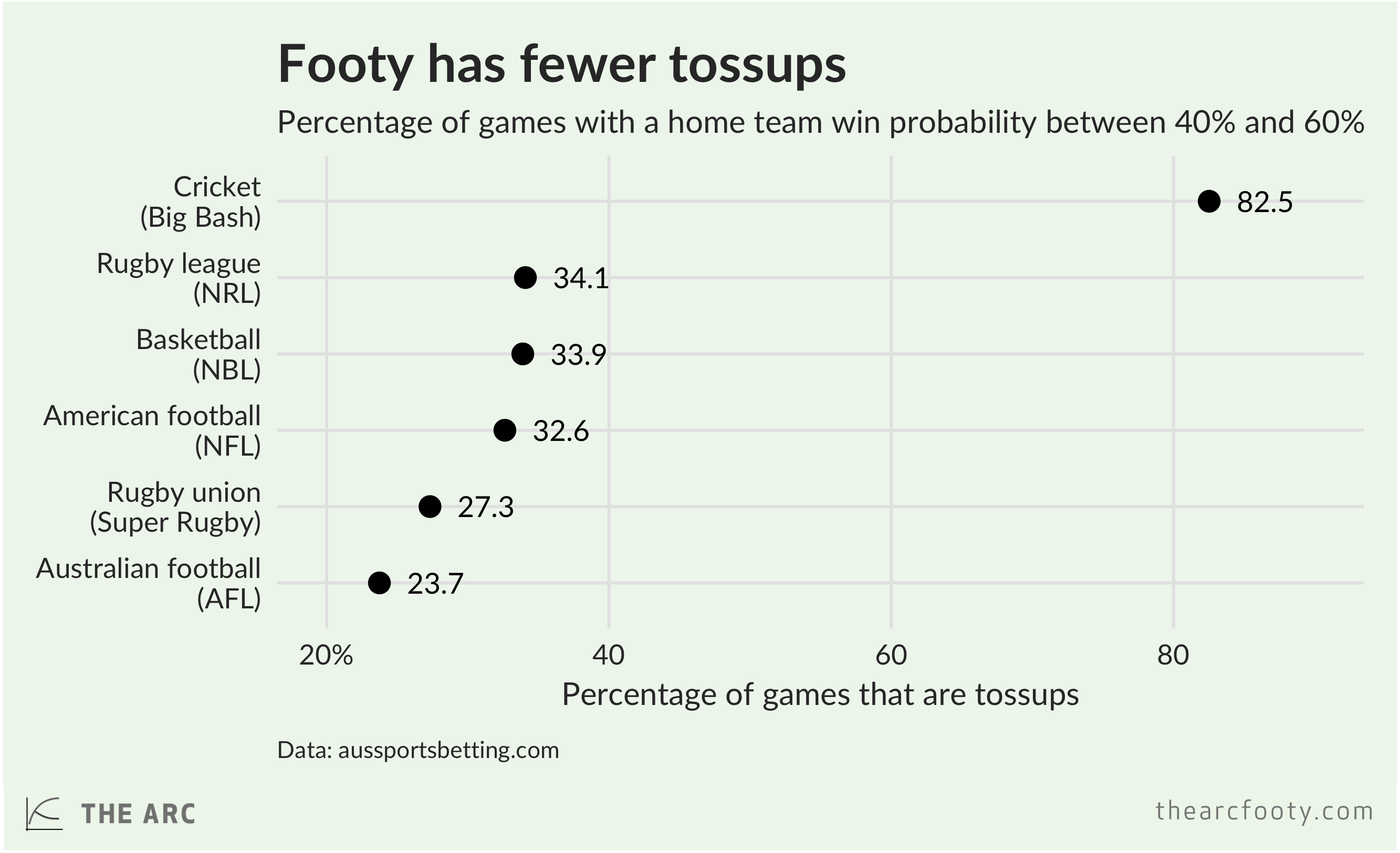
What proportion of games do we want to be tossups? In part, that’s a matter of taste. To me, the BBL figure is too high – Twenty20 cricket games have the feel of a coin toss, in which the result is random and arbitrary. That’s not a lot of fun to me. On the other hand, maybe the AFL figure is a little lower than ideal. Despite the league’s aggressive equalisation policies, there are too few matches with a highly uncertain outcome. The league should be alert to this and resist any pressure from the big, rich clubs to reduce the amount of equalisation in place. Any backsliding would cause there to be even fewer tossup footy games.
- All betting odds were collected from aussportsbetting.com. The probability of a home win was calculated as
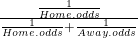. For example, if the bookies’ odds for a home win were quoted as 1.51, with an away win at 2.60, the probability of a home win is calculated as 
.
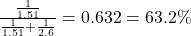The odds for each sport start in:
