Max Barry, creator of the Squiggle and all-round tops guy, has been keeping track of how various footy tipping models have gone this year, including my Elo model. It was a tough year for tipping!
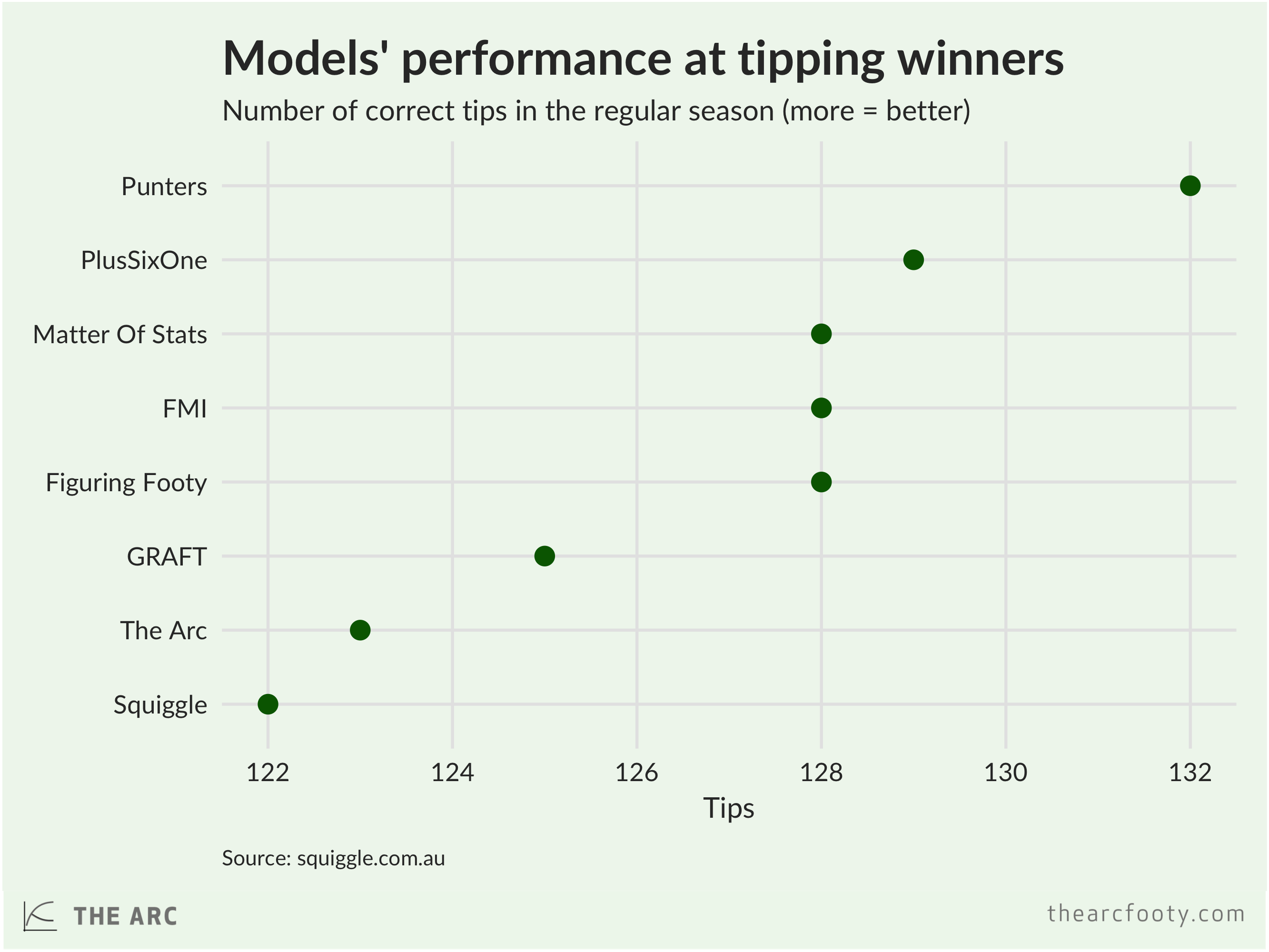
My model didn’t do very well at tipping winners, getting just 123 tips right. That’s the second worst among the models that Max tracked. The betting markets (‘punters’) beat all the models.
But my model did quite well at probabilistic tipping, as measured using ‘bits’. For each game, I (and other modellers) assign each team a chance a victory – for example, my model thinks the Tigers are about 67% likely to win their Preliminary Final.
Probabilistic tipping sounds a bit wonky, but it’s not that complicated. If you are very confident about a tip – say you assign a team a 90% probability of winning – and get it right, you get awarded with a lot of bits, but you’ll lose a lot if you get it wrong. If you’re not very confident about a tip – say you assign a team a 52% chance of winning – then you will gain only a small amount of bits if they win, and only lose a few bits if the team loses.
My model did the best out of the models at probabilistic tipping.

My model also did quite well at tipping margins, ending up with the best margin-tipping performance among the models tracked by Squiggle. The accuracy of margin tipping is measured using the ‘mean absolute error’ between the tipped margin and the actual margin. Let’s say you tipped Port to beat the Eagles by 10 points, but they actually lost by 2 points. In that case, the absolute error on your tips is 12 points. The mean absolute error is just the average of the tipping errors across all games.

There’s a hell of a lot of luck in tipping, particularly in a season as crazy as 2017. I strongly, strongly suspect that if we run this for another few seasons, other models (most likely the excellent Matter of Stats) would come out on top. Still, I’m happy to have ended the home-and-away season with the best record at tipping probabilities and margins, even if the actual tipping figures were a bit woeful. I’d probably rather have my model perform well at tipping probabilities and margins and perform poorly at tipping winners than the other way around.
